Given:
Density of the solid part = 6.23 x 10³ kg/m³
Let's find the fraction of the specimen's apparent volume that is solid.
Apply the formula:
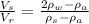
Where:
Vs is the volume of solid in rock
Vr is the volume of rock.
ρa = 1.275 kg/m³
ρw is the density of water = 1000 kg/m³
ρs is the density of solid rock = 6.23 x 10³ kg/m³
Plug in the values in the equation and solve.
We have:
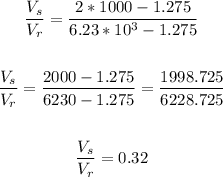
Therefore, the fraction of the specimen's apparent volume that is solid is 0.32
ANSWER:
0.32