Question

An object moves with constant acceleration 3.00 m/s2 and over a time interval reaches a final velocity of 13.0 m/s.(a) If its original velocity is 6.50 m/s, what is its displacement during the time interval? m(b) What is the distance it travels during this interval? m(c) If its initial velocity is −6.50 m/s, what is its displacement during this interval? m(d) What is the total distance it travels during the interval in part (c)? m

Answer 1

Since the object is moving at constant acceleration this is an uniformly accelerated motion and then we can use the following equations:

`v_f^2-v_0^2=2a\Delta x`

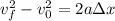
a)

In this case the initial velocity is 6.50 m/s, the final velocity is 13.0 m/s and the acceleration is 3.00 m/s², then we have:

`\begin{gathered} \Delta x=((13)^2-(6.5)^2)/(2(3)) \\ \Delta x=21.13 \end{gathered}`

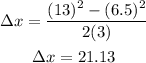
Therefore, the displacement during this time interval is 21.23 m

b)

Since the object was moving in the positive direction from the beginning the distance is equal to the displacement; therefore, the distance during this time interval is 21.23 m

c)

In this case the initial velocity is -6.50 m/s, the final velocity is 13.0 m/s and the acceleration is 3.00 m/s², then we have:

`\begin{gathered} \Delta x=((13)^2-(-6.5)^2)/(2(3)) \\ \Delta x=21.13 \end{gathered}`

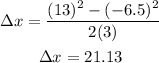
Therefore, the displacement during this time interval is 21.23 m

d)

In this case we need to calculate the distance in two parts; first we need to calculate how much the object moves while its moving to the left until it stops; for this part the initial velocity is -6.50 m/s and the final velocity is zero, then we have:

`\begin{gathered} \Delta x=(0^2-(-6.5)^2)/(2(3)) \\ \Delta x=-7.04 \end{gathered}`

Now we need to determine the displacement from when the velocity is zero until it reaches 13 m/s, then we have:

`\begin{gathered} \Delta x=(13^2-0^2)/(2(3)) \\ \Delta x=28.17 \end{gathered}`

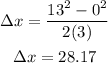
Finally we add the absolute value of this displacements to calculate the distance:

`d=7.04+28.17=35.21`

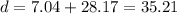
Therefore, the distance the object travelled is 35.21 m