Question

A ball is thrown vertically upward. after t seconds, it’s height (in feet) is given by the function h (t)=108t-16t^2. What is the maximum height the ball will reach?

Answer 1

Function h(t) gives us the height as a function of time.

`h(t)=108t-16t^2`

Notice that h(t) is a parabola that opens downwards on the plane; therefore, it will have only one critical point and that critical point will be a maximum.

To find the critical point of the function, we need to find its derivative as shown below

`\begin{gathered} h^(\prime)(t)=108-2\cdot16t=108-32t \\ \Rightarrow h^(\prime)(t)=108-32t \end{gathered}`

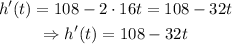
Then, set h'(t)=0 and solve for t

`\begin{gathered} h^(\prime)(t)=0 \\ \Rightarrow108-32t=0 \\ \Rightarrow t=(108)/(32)=(27)/(8) \\ \Rightarrow t=(27)/(8) \end{gathered}`

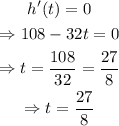
Finally, evaluate h(27/8) to obtain the answer

`\begin{gathered} h((27)/(8))=108((27)/(8))-16((27)/(8))^2=(729)/(2)-(729)/(4)=(729)/(4) \\ \Rightarrow h((27)/(8))=(729)/(4)=182.25 \\ \end{gathered}`

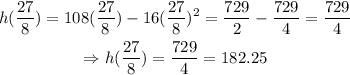
The answer is 182.25 ft.