You have the following function:
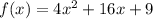
In order to find the zeros of the previous function, use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this case you have:
a = 4
b = 16
c = 9
replace the previous values into the quadratic formula:
![\begin{gathered} x=\frac{-(16)\pm\sqrt[]{(16)^2-4(4)(9)}}{2(4)} \\ x=\frac{-16\pm\sqrt[]{112}}{8} \\ x=(-16\pm10.58)/(8) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tbt0fsyv0q9uvdblu0vcwl96w3nhz3gz1b.png)
Then, you have the following values for x:
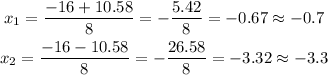
Hence, the solution to the given function are:
x1 = -0.7
x2 = -3.3