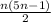Solution
Show that the following is true by mathematical induction for all natural numbers of n
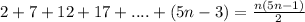
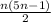
when n = 1,
The claim is true for n = 1, a_1 = 2
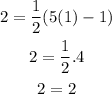
Assume the claim is true for n , and look for n+1

The induction hypothesis is that the first n terms sum up to: