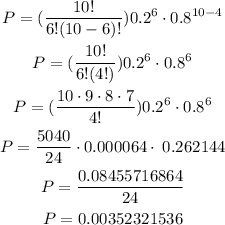Okay, here we have this:
Here we are going to use the binomial probability equation to solve the problem, so we have the following formula:
Where:
n=total number of questions (trials)=10
k=number correct (successes)=6
n−k=number incorrect (failures)=4
p=probability of getting 1 question correct=(0.2)
q=1−p probability of getting 1 question incorrect=(0.8)
So we obtain the following:

Replacing: