Question

Suppose a small fish species is introduced into a pond that had not previously held this type of fish, and that its population P, in thousands, is modeled by P=(3x+1)/(x+4) where x represents the time in months. i) Describe the overall trend of P as x goes to infinity. ii) how many fish were initially introduced into the pond? iii) this model is restricted to x>=0. Why?

Answer 1

i)When x goes to infinity we get:

`\lim _(x\rightarrow+\infty)P(x)=\lim _(x\rightarrow+\infty)(3x+1)/(x+4)`

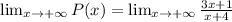
Computing the limit we get:

`\lim _(x\rightarrow+\infty)(3x+1)/(x+4)=\lim _(x\rightarrow+\infty)((3x)/(x)+(1)/(x))/((x)/(x)+(4)/(x))=\lim _(x\rightarrow+\infty)(3+(1)/(x))/(1+(4)/(x))=(3+0)/(1+0)=3`

Therefore the fish population tends to 3,000 fishes as x goes to infinity.

ii) The initial population is:

`P(0)=(3\cdot0+1)/(0+4)=(1)/(4)`

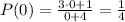
which is equal to 1000/4=250 fishes.

iii) This model is restricted to x≥0 because there were no fishes of the same type in the pond before the introduction of the species.