We have to find a point that is a solution to the following inequality:
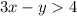
We can rearrange this to assign a value to x and then find a value of y that makes the point be a solution.
We can rearrange it as:
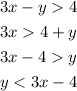
Then, we can assign a value to x, like x = 0, and find the range of values that satisfy the inequality when x = 0:
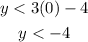
This means that if x = 0, then y has to be less than -4. Then, for example, (0,-6) is a solution to the inequality.
We can see it in a graph as:
The red shaded region is the solution region. Any point in this regions is a solution to the inequality. The dashed line is the line 3x-y = 4.
We can also check with the values of x and y in the inequality:
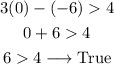
As it is true, we know that the point is part of the solution region.
Answer: one solution to the inequality is (0,-6).