Question

A certain community consists of 4700 people, and one individual has a particularly contagious strain of influenza. Assuming the community has not had vaccination shots and are all susceptible, the spread of the disease in the community is modeled byA=4700/1+4699e^-0.3twhere A is the number of people who have contracted the flu after t days.(a) How many people have contracted the flu after 9 days? Round your answer to the nearest whole number.(b) What is the carrying capacity for this model?(c) How many days will it take for 675 people to contract the flu? Round your answer to the nearest whole number.

Answer 1

a) 15 people

b) 4700 people

c) 22days

Explanations:

Given the exponential function that models the spread of a disease in a community expressed as:

`A=(4700)/(1+4699e^(-0.3t))`

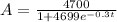
where:

A is the number of people who have contracted the flu after t days.

a) To know the number of people that have contracted after 9days, we will substitute t = 9 into the formula as shown:

`\begin{gathered} A=(4700)/(1+4699e^(-0.3(9))) \\ A=(4700)/(1+4699(0.06721)) \\ A=(4700)/(1+315.7897) \\ A=(4700)/(316.7987) \\ A=14.8\approx15people \end{gathered}`

Hence about 15people will have contracted the flu after 9days

b) The carrying capacity of the model is the maximum population that the community can support indefinitely, given the available resources.

In order to determine the carrying capacity, we will substitute t as ∞ and calculate the equivalent population

`\begin{gathered} A=(4700)/(1+4699e^(-0.3(\infty))) \\ A=(4700)/(1+(4699)/(e^(\infty))) \\ A=(4700)/(1+0) \\ A=4700 \end{gathered}`

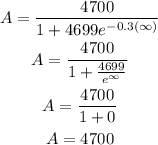
Hence the carrying capacity for the model is 4700 populations

c) In order to calculate the number of days it take for 675 people to contract the flu, we will substitute A = 675 and calculate the value of "t"

`\begin{gathered} 675=(4700)/(1+4699e^(-0.3t)) \\ 675(1+4699e^(-0.3t))=4700 \\ 1+4699e^(-0.3t)=(4700)/(675) \\ 1+4699e^(-0.3t)=6.9629 \\ 4699e^(-0.3t)=5.9629 \\ e^(-0.3t)=0.001269 \end{gathered}`

Take the natural logarithm of both sides

`\begin{gathered} lne^(-0.3t)=ln(0.001269) \\ -0.3t=ln(0.001269) \\ -0.3t=-6.6695 \\ t=(6.6695)/(0.3) \\ t=22.23\approx22days \end{gathered}`

Hence it will take approximately 22 days for 675 people to contract the flu