The variables given are the fixed cos (called the flat fee) which is a known variable, that is 75. You also have the variable cost which can change as the mileage increases and that is 0.55 per mile driven.
If the total cost at 1 mile is given as
75.55 = flat fee + fee per mile driven, then the equation would be as follows;
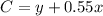
Where C is the total cost, y is the flat fee (which does not change) and x is the number of miles driven. This can now be properly expressed as

That is the answer to part (a)
(b) The total cost of renting and driving the truck for 60 miles can now be calculated as follows;
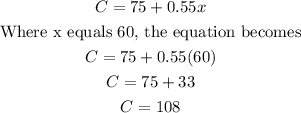
The cost therefore of renting and driving the truck for 60 miles is $108