The mean recovery time is 3 days.
The standard deviation is 1.5 days.
Part a:
Assuming a normal distribution, we have:
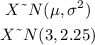
Part b:
Since it is a normal distribution, the median must be the same as the mean, that is 3 days.
Part c:
For a recovery time of 4.7 days, we have:
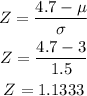
Part d:
The Z-score for a recovery time of 2.3 days is given by:
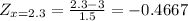
Then, according to a normal table, we have:
P(X > 2.3) = P(Z > -0.4667) = 0.6808
Part e:
The Z-score for 4 is given by:

Then we have:
[tex]P(4Part f:
According to the normal distributrion, the 75th percentile for recivery time is close to Z = 0.66, which corresponds to 4 days.