Question

I have a calculus question about linear approximation, pic included

Answer 1

Given:

`\begin{gathered} f(x)=\sqrt[3]{x} \\ \\ \text{ Tangent line t f\lparen x\rparen at x = 27} \end{gathered}`

Apply the slope-intercept form:

y = mx + b

Where m is the slope and b is the y-intercept.

• Let's find the derivative of f(x):

`\begin{gathered} f^(-1)(x)=(d)/(dx)(x)^{(1)/(3)}=(1)/(3)(x^{(1)/(3)-1}) \\ \\ f^(-1)(x)=(1)/(3)x^{-(2)/(3)} \end{gathered}`

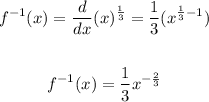
• Now, let's find f'(27):

`\begin{gathered} f^(\prime)(27)=(1)/(3)(27)^{-(2)/(3)} \\ \\ f^(\prime)(27)=\frac{(1)/(3)}{\sqrt[3]{27}^2}=((1)/(3))/(3^2)=((1)/(3))/(9)=(1)/(3*9)=(1)/(27) \\ \\ f^{^(\prime)}(27)=(1)/(27) \end{gathered}`

Thus, we have:

Slope, m = 1/27

• The equation of through (27, 3) and has a slope of 1/27 will be:

`\begin{gathered} y-3=(1)/(27)(x-27) \\ \\ y-3=(1)/(27)x-(1)/(27)*27 \\ \\ y-3=(1)/(27)x-1 \\ \\ y=(1)/(27)x-1+3 \\ \\ y=(1)/(27)x+2 \end{gathered}`

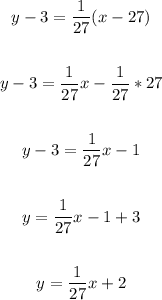
Therefore, the equation of the tangent line is:

`\begin{gathered} y=(1)/(27)x+2 \\ \\ \text{ Where:} \\ m\text{ = }(1)/(27) \\ \\ b=2 \end{gathered}`

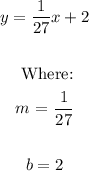
To find the approximation, we have:

`\begin{gathered} \sqrt[3]{27.2}=f(27.2) \\ \\ f(x)=(1)/(27)x+2 \\ Where\text{ x = 27.2} \\ Substitute\text{ 27.2 for x.} \\ \\ f(27.2)=(1)/(27)(27.2)+2 \\ \\ f(27.2)=(27.2)/(27)+2 \\ \\ f(27.2)=1.0074+2 \\ \\ f(27.2)=3.0074 \end{gathered}`

ANSWER:

`\begin{gathered} m=(1)/(27) \\ \\ b=2 \\ \\ \sqrt[3]{27.2}=3.0074 \end{gathered}`