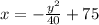Question

A comet follows a parabolic path with directrix x = 85 and vertex at (75, 0).Write the equation of the comet's path in standard form. Show your work.Note: This deals with Pre-Calculus Conic Sections

Answer 1

Since we have a vertical line as the directrix(x = 85) with a vertex to its left side, we're dealing with a parabola open to the left, therefore, the standard form equation for this parabola is given by

`x=a(y-k)^2+h`

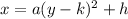
Where (h, k) are the vertex coordinates.

The vertex is the midpoint between the focus and the directrix, this means the focus of our parabola is (65, 0).

The distance between any point of the parabola and the directrix is the same distance between this same point to the focus. Then, we can use this information to calculate our equation.

The distance between any point to the focus is given by

`d((x,y),(65,0))=\sqrt[]{(x-65)^2+y^2}`

And the distance between any point to the directrix is given by

`d((x,y),x=85)=\sqrt[]{(x-85)^2}`

Since those values are equal, we have

`\sqrt[]{(x-65)^2+y^2}=\sqrt[]{(x-85)^2}`

Expanding this equation, we have

`\begin{gathered} \sqrt[]{(x-65)^2+y^2}=\sqrt[]{(x-85)^2} \\ (x-65)^2+y^2=(x-85)^2 \\ x^2-130x+65^2+y^2=x^2-170x+85^2 \\ y^2+65^2=-40x+85^2 \\ y^2+65^2-85^2=-40x \\ y^2-3000=-40x \\ -(y^2)/(40)+75=x \\ x=-(y^2)/(40)+75 \end{gathered}`

And this is our equation in standard form.

`x=-(y^2)/(40)+75`