Question

What is the change in pressure on an adrenaline junkie who scuba dives at a depth of 24 m in seawater one day and parachutes at an altitude of 7.5 km the next day? Give the absolute value and assume at the average air density within the altitude range is 0.870 kg/m³

Answer 1

The pressure exerted on an object immersed on a fluid is given by:

`P=\rho gh`

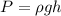
where rho is the density, g is the gravitational acceleration and h is the depth or height of the object in the fluid.

The denisty of sea water is 1026 kg/m^3 and we know the depth in this case is 24 m, then we have:

`\begin{gathered} P_w=\left(1026\right)\left(24\right)\left(9.8\right) \\ P_w=241315.2 \end{gathered}`

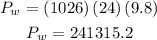
Hence the pressure in water is 241315.2 Pa.

For the air we know the density is 0.870 kg/m^3, the height is 7.5 km, then we have:

`\begin{gathered} P_a=\left(0.870\right)\left(9.8\right)\left(7.5*10^3\right) \\ P_a=63945 \end{gathered}`

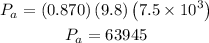
Now, that we know this we can calculate the change in pressure:

`\begin{gathered} \Delta P=240844.8-63945 \\ \Delta P=177370.2 \end{gathered}`

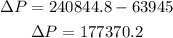
Therefore, the change in pressure is 177370.2 Pa.