For the volume of a triangular prism, we have the following formula:
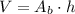
where A_b is the area of the base and h is the height of the prism. Let's first calculate the area of the base of the prism. In this case, we have that:
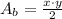
Where x=19 and y =9, then:
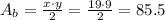
Now that we have the area of the base, we can easily calculate the volume:
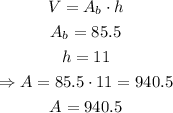
Therefore, the volume of the prism is 940.5 yd^3