Given in the problem that the coordinates of the end points of a side of a rectangle is;
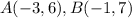
Each of the angles of a rectangle is 90 degrees. Let a line BC be perpendicular to line AB.
The slope of line AB is;
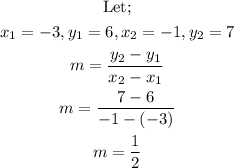
When the two lines are perpendiculat to each other, the product of their slopes is negative one.
Hence, the slope of line BC is;
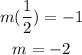
Now, we can get the coordinate of point C (x,y). We have;
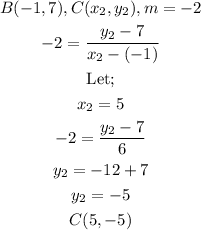
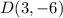
This is a rectangle because the two sides are parallel to each other and opposite sides are equal in length.