Answer
a) Probability that there are 3 drug overdoses in a random night = 0.055
b) Probability that there are at most 3 drug overdoses in a random
night = 0.087
Step-by-step explanation
The Poisson distribution will be used to solve this one.
The Poisson distribution is given as
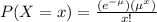
where
x = actual variable whose probability we want to find = 3 drug overdoses in one night
μ = mean of the distribution = 6.9 drug overdoses per night

b) For the probability of at most 3 drug overdoses in one night,
P (X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
For each of them,
μ = 6.9
But for x, we will calculate for each of them using
x = 0, x = 1, x = 2, x = 3
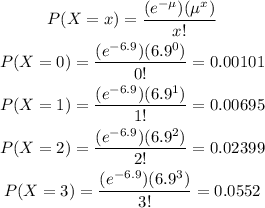
P (X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
P (X ≤ 3) = 0.00101 + 0.00695 + 0.02399 + 0.0552 = 0.08714 = 0.087
Hope this Helps!!!