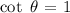Question

Find the value of the six trigonometric functions for 0please help

Answer 1

Here, we want to get the values of the six trigonometric functions

Firstly, we need the measure of the third side of the triangle

Let us call this third side x

Mathematically, the square of the hypotenuse ( 4 root 2) is equal the sum of the two other sides

The above is the Pythagoras' theorem

Thus, we have it that;

`\begin{gathered} (4\sqrt[]{2})^2=4^2+x^2 \\ 32=16+x^2 \\ x^2=\text{ 32-16} \\ x^2\text{ = 16} \\ x\text{ = 4} \end{gathered}`

Thus, we have the opposite and the hypotenuse as 4

We start calculating the functions as follows;

a) Sine

This is the ratio of the opposite to the hypotenuse.

`\sin \text{ }\theta\text{ = }\frac{4}{4\sqrt[]{2}}\text{ = }\frac{\sqrt[]{2}}{2}`

b) Cosine

This is the ratio of the adjacent to the hypotenuse

Since the adjacent value id equal to the opposite, we have the sine and cosine equal

`\text{cos }\theta\text{ = }\frac{4}{4\sqrt[]{2}\text{ }}\text{ = }\frac{\sqrt[]{2}}{2}`

c) Tangent

This is the ratio of the opposite to the adjacent

We have this as;

`\text{Tan }\theta\text{ = }(4)/(4)\text{ = 1}`

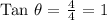
d) Secant

This is the reciprocal of the cosine

Mathematicaly, it is the ratio of the hypotenuse to the adjacent

We have this as;

`\sec \text{ }\theta\text{ = }\frac{4\sqrt[]{2}}{4}\text{ = }\sqrt[]{2}`

e) Cosecant

This is the ratio of the hypotenuse to the opposite

Mathematically, we have this as;

`co\sec \text{ }\theta\text{ = }\frac{4\sqrt[]{2}}{4}\text{ = }\sqrt[]{2}`

f) Cot

This is the reciprocal of tan

It is the ratio of adjacent to the opposite

We have this as;

`\cot \text{ }\theta\text{ = 1}`