Question

If the width of a rectangular prism is doubled, the length is tripled, and the height is doubled, what is the volume of the resulting rectangular prism? A. double the original volumeB. six times the original volumeC. twelve times the original volumeD. triple the original volume

Answer 1

Consider a rectangular prism with length l, width w and height h;

Volume of rectangular prism = Length x width x height

`\text{Volume of the rectangular prism =lwh}`

Now, it is given that, If the width of a rectangular prism is doubled;

new width = 2w

the length is tripled, i,e

New length = 3l

The height is doubled i.e,

New height = 2h

The volume of the rectangular prism is;

`\begin{gathered} \text{Volume of new prism = length }*\text{width }*\text{ height} \\ \text{Volume of new prism =3l}*2w*2h \\ \text{Volume of new prism =}3*2*2lwh \\ \text{Volume of new prism =}12\text{lwh} \end{gathered}`

Since, volume of original prism is lwh

Thus,

`\begin{gathered} \text{Volume of new prism =}12\text{lwh} \\ \text{Volume of new prism =}12\text{Volume of original prism} \end{gathered}`

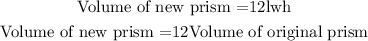
Thus, the resulting volume of the prism is twelve times the original volume

Answer : C) twelve times the original volume