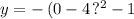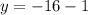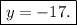Question

I know how to The vertex but I’m not sure how to do it when there is a negative sign outside of the ()s

Answer 1

Vertex: ( 4, -1)

Step-by-step explanation:

The vertex form of a parabola is given by

`f\mleft(x)=a\left(x-h\right)^2+k\mright)`

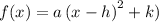
where is the location of the vertex is (h, k).

Now in our case. we have

`f\mleft(x\mright)=-\left(x-4\right)^2-1`

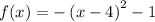
From the above equation we recognize h = 4 and k = - 1; therefore, the vertex is

`\left(4,-1\right)`

which is our answer!

Let us now find the x-intercepts.

To find the x-intercepts, we solve the following.

`0=-\left(x-4\right)^2-1`

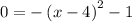
The first step is to add + 1 to both sides. This gives

`1=-(x-4)^2`

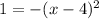
The next step is to multiply both sides by - 1.

`-1=(x-4)^2`

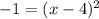
Then we take the square root of both sides. This gives

`√(-1)=√(\left(x-4\right)^2)`

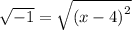
On the left, we see that we are taking the sqaure root of a negative number. This cannot be done since it gives imaginary ( and not real) numbers.

Hence, we conclude that the solutions to 0 = -(x - 4)^2 - 1 do not exist, and therefore, the parabola has no x-intercepts.

To find the y-intercept, we put x = 0 into our equation. This gives

`y=-\left(0-4\right?^2-1`
`y=-16-1`
`\boxed{y=-17.}`