Question

ISolve the following equation for x:0 . 4 ( 2 + 12 ) = 3 [ 0 . 2 + ( − 2 ) ] − 4

Answer 1

We are given the following equation:

`0.4(2x+(1)/(2))=3(0.2x+(-2))-4`

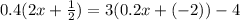
First, we will use the distributive property:

`0.8x+0.2=0.6x+3(-2)-4`

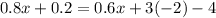
Now, we solve the product 3(-2):

`0.8x+0.2=0.6x-6-4`

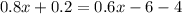
Now, we add like terms:

`0.8x+0.2=0.6x-10`

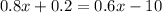
Now, we will subtract 0.6x from both sides:

`\begin{gathered} 0.8x-0.6x+0.2=0.6x-0.6x-10 \\ 0.2x+0.2=-10 \end{gathered}`

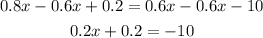
Now, we will subtract 0.2 from both sides:

`\begin{gathered} 0.2x+0.2-0.2=-10-0.2 \\ 0.2x=-10.2 \end{gathered}`

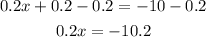
Now, we divide both sides by 0.2:

`x=-(10.2)/(0.2)`

Solving the operation:

`x=-51`

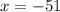
Therefore, the value of "x" is -51.