Question

State the postulate or theorem and which lines are parallel

Answer 1

Step 1

Corresponding angles are the angles that are formed when two parallel lines are intersected by the transversal. The opening and shutting of a lunchbox, solving a Rubik's cube, and never-ending parallel railway tracks are a few everyday examples of corresponding angles. These are formed in the matching corners or corresponding corners with the transversal.

Step 2

We are given;

`\begin{gathered} \angle1\cong\angle3 \\ \angle2\cong\angle5 \\ \angle3\cong\angle10 \end{gathered}`

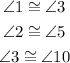
Since, we know that If two lines and a transversal form alternate interior angles that are congruent, then the two lines are parallel.

`\angle2\cong\angle5(\text{ Alternate interior angles\rparen}`

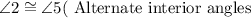
The lines in connection with this are;

`\begin{gathered} Transversial\text{ is l and the two parrallel line are j and k} \\ \end{gathered}`

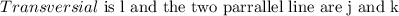
Reason; If two lines and a transversal form alternate interior angles that are congruent, then the two lines are parallel.

Step 3

We are also given;

`\angle1\cong\angle3(corresponding\text{ angles\rparen}`

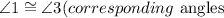
We know that If a transversal intersects two parallel lines, the corresponding

angles are congruent.

`\begin{gathered} The\text{ transversal is l and the parallel lines are j and k} \\ Hence\text{ again l,j nd k are parallel} \end{gathered}`

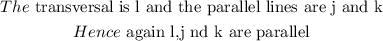
Also;

`\angle3\cong\angle10(Alternate\text{ exterior angles \rparen}`

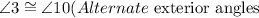
We know that If a transversal intersects two parallel lines, then alternate

exterior angles are congruent.

`Transversal\text{ is K and the parallel lines are l and m}`

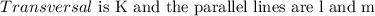
Therefore all four lines j,k,l, and, m are parallel lines. The reasons are;

1) If two alternate exterior angles are congruent then for this to be true a transversal must intersect 2 parallel lines

2) If two alternate interior angles are congruent then for this to be true a transversal must intersect two parallel lines

3) If two corresponding angles are congruent then for this to be true a transversal must intersect two parallel lines.