![y = 1.5x+5\implies y=\cfrac{3}{2}x+5\implies \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{2}}{2(y)=2\left( \cfrac{3}{2}x+5 \right)} \\\\\\ 2y=3x+10\implies -3x+2y=10 \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{rrrrr} 3x&-&2y&=&7\\ -3x&+&2y&=&10\\\cline{1-5} 0&+&0&=&17 \end{array}\qquad \impliedby \textit{another way of saying \underline{no solutions}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/j9t0f2gxdvuhvb45ittx7pyu62wcmtnk84.png)
well, again, if we were to solve for "y" on each and put them in slope-intercept form, we'd get
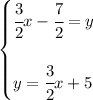
as you can see, they have the same slope, meaning the lines are parallel to each other, however the y-intercept is different, so these are two parallel lines with a gap in between, and parallel lines with a gap never touch each other, thus no intersections and thus no solutions.