AB=10
1) Considering that similar triangles, have congruent angles and proportional sides, and considering that the line segment ED, is parallel to the line segment BC
2) Then we can state that
m∠AED ≅ m∠ACB because they are corresponding angles.
Having said that, we found the measure of AB, by writing a proportion between the sides of the smaller triangle and the larger one. So AD (smaller one) = 6 and its corresponding AB (Larger one) = 6 +x.
And ED (smaller) over BC (larger)
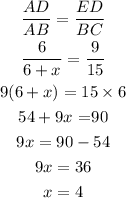
3) Hence, the side AB, is
AB = 6 +x
AB = 6+4
AB=10