The rational zeros theorem states that the possible zeros of a polynomial can be found through the division of the factors of the constant term by the leading coefficient factors.
In this case,
the leading coefficient is: 1
The constant term is: 12
The factors for the leading coefficient are: ±1
The factors for the constant term are: ±1, ±2, ±3, ±4, ±6, ±12.
The possible roots are:
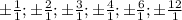
Answer:
-1, 1, -2, 2, -3, 3, -4, 4, -6, 6, -12, 12.