y = 1/2x + 8
y = cx + 10
In the system of equations above, c is a constant. If
the system has no solution, what is the value of c?
so, y=y
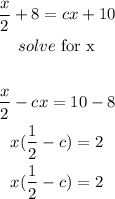
this equation is indefinde when 1/2 - c= 0, there is not value for x that makes the equation true
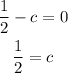
so, the value of c =0.5