Question

Use the elimination method when solving the translated system Two angles are (complementary angles are angles whose sum is 90.) Their difference is 40. Find the angles. The larger angle is ? , and the smaller angle is ?.

Answer 1

Let's write the equation system first. We have two angles, let's call the, A and B, wich are complementary. This is:

`A+B=90º`

Also their difference is 40º:

`A-B=40º`

The system is;

`\begin{cases}A+B=90º \\ A-B=40º\end{cases}`

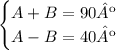
Now, if we add the two equations, since we have a "B" and a "-B", they will eliminate:

`\begin{gathered} (A+B=90º)+(A-B=40º) \\ A+B+A-B=90º+40º \\ A+A+B-B=130º \\ 2A=130º \\ A=(130º)/(2)=65º \end{gathered}`

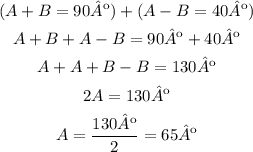
The value of one of the angles is 65º. To find the other angle, we can go back to the first equation, A + B = 90º:

`65º+B=90º`

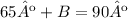
And solve:

`B=90º-65º=25º`

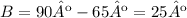
The larger angle is 65º and the smaller angle is 25º