Question

The amount of particulate pollution p in the air depends on the wind speed s, among other things, with the relationship between p and s approximated by p=25-0.01s^2, where p is in ounces per cubic yard and s in miles per hour. what is the amount of particulate pollution when there is no wind? what would the wind speed have to be to have no particulate pollution?

Answer 1

If there is no wind, then s = 0. Substituting into the equation:

`\begin{gathered} p=25-0.01\cdot0^2 \\ p=25 \end{gathered}`

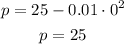
The amount of particulate pollution when there is no wind is 25 ounces per cubic yard.

If there is no particulate pollution, then p = 0. Substituting into the equation:

`0=25-0.01s^2`

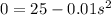
The expression on the right is a difference of squares. Taking the square root of each term:

`\begin{gathered} \sqrt[]{25}=5 \\ \sqrt[]{0.01s^2}=\sqrt[]{0.01}\sqrt[]{s^2}=0.1s \end{gathered}`

Recalling the equation:

`0=(5-0.1s)(5+0.1s)`

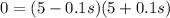
This equation has two solutions:

`\begin{gathered} 5-0.1s=0 \\ 5-0.1s+0.1s=0+0.1s \\ 5=0.1s \\ (5)/(0.1)=(0.1s)/(0.1) \\ 50=s \end{gathered}`

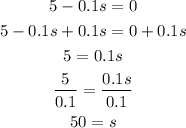
Or:

`\begin{gathered} 5+0.1s=0 \\ 5=-0.1s \\ (5)/(-0.1)=s \\ -50=s \end{gathered}`

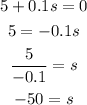
Wind speed cannot be negative, then the last solution is discarded.

The wind speed has to be 50 miles per hour to have no particulate pollution.