At some point along the direct path from the center of the Earth to the center of the Moon, the gravitational force of attraction on a spacecraft from the Moon becomes greater than the force from the Earth.
(a) How far from the center of the Earth does this occur?
The distance from the center of the Earth to the point at which the gravitational force of attraction from the Moon is greater than the force from the Earth is given by
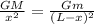
Where M is the mass of the Earth.
m is the mass of the Moon.
G is the gravitational constant.
L is the distance between the Earth and the Moon.
x is the distance that we need to find out.
Let us simplify the above equation,
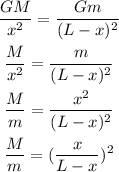
The ratio of Earth's mass to the Moon's mass is (M/m = 81)

The distance between the Earth and the Moon is L = 384400 km
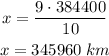
Therefore, the gravitational force of attraction on a spacecraft from the Moon becomes greater than the force from the Earth at a distance of 345960 km from the center of the Earth does this occur.
(b) At this location, how far is the spacecraft from the surface of the Moon?
The distance between the spacecraft from the surface of the Moon is given by
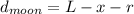
Where r is the radius of the Moon that is 1740 km
Substituting all the known values into the above equation, we get

Therefore, the distance between the spacecraft from the surface of the Moon is 36700 km
How far is it from the surface of the Earth?
The distance between the spacecraft from the surface of the Earth is given by
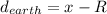
Where R is the radius of the Earth that is 6370 km
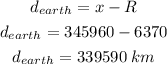
Therefore, the distance between the spacecraft from the surface of the Earth is 339590 km