1 Answer

Dmubu · Answer 1 · 2023-07-31T06:44:35+0000

The given system of equations is:

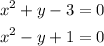
$\begin{gathered} x^2+y-3=0 \\ x^2-y+1=0 \end{gathered}$

Add the two equations to eliminate the variable y:

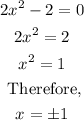
$\begin{gathered} 2x^2-2=0 \\ 2x^2=2 \\ x^2=1 \\ \text{ Therefore,} \\ x=\pm1 \end{gathered}$

Substite x = 1 into the first equation:

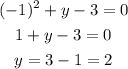
$\begin{gathered} (-1)^2+y-3=0 \\ 1+y-3=0 \\ y=3-1=2 \end{gathered}$

Subtitute x=-1 into the second equation:

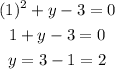
$\begin{gathered} (1)^2+y-3=0 \\ 1+y-3=0 \\ y=3-1=2 \end{gathered}$

Therefore, the points (-1, 2) and (1, 2) are solutions of the system.

The graph of the system is:

Please log in or register to add a comment.