Question

A beam of red light is incident at an angle of 54.3 o on an equilateral prism. If the index of refraction of red light is 1.400, at what angle does the beam emerge from the other face of the prism?

Answer 1

35.57°

Step-by-step explanation

Given:

• The incident angle, θ₁ = 54.3°

,

• The index of refraction of red light in this prism, n₃ = 1.4

Find:

• The angle at which the beam emerges from the other face of the prism, θ₂

We have the following situation,

Using Snell's law, we can find the angle α₁,

`n_1\sin\theta_1=n_3\sin\alpha_1`

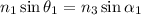
Solving for α₁,

`\alpha_1=\sin^(-1)\left((n_1)/(n_3)\sin\theta_1\right)=\sin^(-1)\left((1)/(1.4)\sin54.3\degree\right)\approx35.45\degree`

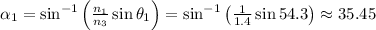
Now, to find the angle at which the beam emerges from the other face of the prism, we have to find angle α₂, which would be the incidence angle for the second refraction.

Let's go back to the diagram of the prism,

At the top, the beam of light forms a triangle. We know that the sum of the interior angles of any triangle is 180°. We also know that angles α₁ and α₂ are complementary to the other two interior angles of that triangle, so we have,

`(90-\alpha_1)+(90-\alpha_2)+60=180`

Solving for α₂,

`\alpha_2=90+90+60-\alpha_1-180=90+90+60-35.45-180=24.55`

Now, knowing that the incidence angle at the other end of the prism is 24.55°, we can find the refraction angle using Snell's law,

`n_3\sin\alpha_2=n_2\sin\theta_2`

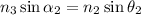
Solving for θ₂,

`\theta_2=\sin^(-1)\left((n_3)/(n_2)\sin\alpha_2\right)=\sin^(-1)\left((1.4)/(1)\sin24.55\degree\right)\approx35.57\degree`

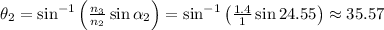
Hence, the beam emerges from the other side of the prism at an angle of 35.57°.