Equation:

The vertex is given by the following formula:
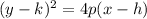
where the vertex is (h, k). Thus, in our equation k = -1 and h = 5, and the vertex
is (5, -1).
Additionally, the focus is given by (h+p, k). In our case:
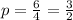
Then, the focus is:
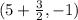
Simplifying:
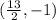
The directrix is x = h - p:

Finally, the axis of symmetry is y = -1.