Question

Finding the vertex focus directrix and axis of symmetry of a parabola

Answer 1

Equation:

`(y+1)^2=6(x-5)`

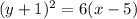
The vertex is given by the following formula:

`(y-k)^2=4p(x-h)`

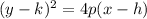
where the vertex is (h, k). Thus, in our equation k = -1 and h = 5, and the vertex

is (5, -1).

Additionally, the focus is given by (h+p, k). In our case:

`p=(6)/(4)=(3)/(2)`

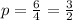
Then, the focus is:

`(5+(3)/(2),-1)`

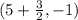
Simplifying:

`((13)/(2),-1)`

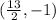
The directrix is x = h - p:

`x=5-(3)/(2)=(7)/(2)`

Finally, the axis of symmetry is y = -1.