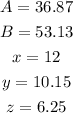Question

Find the values of x, y, z, A, and B in the image below. List the facts that both triangles have 90° angles and that the triangles are similar. What is the value of A and B in degrees? What is the measure of y and z?

Answer 1

`\begin{gathered} A=36.87\text{\degree} \\ B=53.13\text{\degree} \\ x=12 \\ y=10.15 \\ z=6.25 \end{gathered}`

Explanation:

First, we'll work on the triangle that's on the left side. We'll find the values of A,B and x.

Using the law of sines, we'll have that:

`(\sin(90))/(15)=(\sin(A))/(9)`

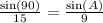
Solving for A,

`\begin{gathered} (\sin(90))/(15)=(\sin(A))/(9) \\ \\ \rightarrow\sin(A)=(9\sin(90))/(15) \\ \\ \rightarrow\sin(A)=(3)/(5) \\ \\ \rightarrow A=\sin^(-1)((3)/(5)) \\ \\ \Rightarrow A=36.87\text{\degree} \end{gathered}`

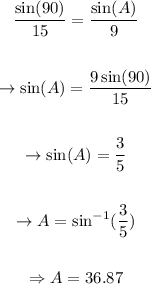
Now, since we know that the sum of the interior angles of a triangle is 180°, we'll have that:

`\begin{gathered} 90+A+B=180 \\ \rightarrow B=180-A-90 \\ \rightarrow B=180-36.87-90 \\ \\ \Rightarrow B=53.13\text{\degree} \end{gathered}`

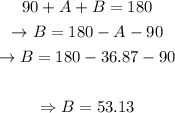
Using the law of sines again, we'll get that:

`(x)/(\sin(B))=(15)/(\sin(90))`

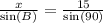
Solving for x,

`\begin{gathered} (x)/(\sin(B))=(15)/(\sin(90)) \\ \\ \rightarrow x=(15\sin(B))/(\sin(90))\rightarrow x=(15\sin(53.13))/(\sin(90)) \\ \\ \Rightarrow x=12 \end{gathered}`

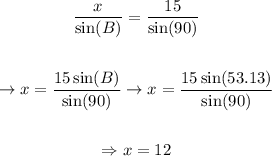
Now, we'll work on the triangle that's on the right side. We'll find the values of y and z.

Since this is a right triangle (it has a 90° angle), we can say that:

`\cos(38)=(8)/(y)`

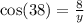
Solving for y,

`\begin{gathered} \cos(38)=(8)/(y)\rightarrow y\cos(38)=8\rightarrow y=(8)/(\cos(38)) \\ \\ \Rightarrow y=10.15 \end{gathered}`

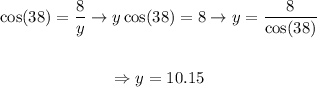
We can also state that:

`\tan(38)=(z)/(8)`

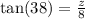
Soving for z,

`\begin{gathered} \tan(38)=(z)/(8)\rightarrow z=8\tan(38) \\ \\ \Rightarrow z=6.25 \\ \end{gathered}`

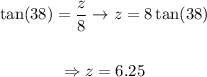
This way, we can conclude that:

`\begin{gathered} A=36.87\text{\degree} \\ B=53.13\text{\degree} \\ x=12 \\ y=10.15 \\ z=6.25 \end{gathered}`