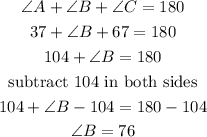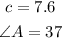
Step-by-step explanation
to solve this we need to use the cosine law
Law of cosines says
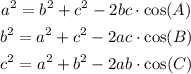
then
Step 1
find c
Let
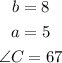
now, let's find c

Step 2
now,let's find the angle A
![\begin{gathered} a^2=b^2+c^2-2bc\cdot\cos (A) \\ replace \\ 5^2=8^2+7.6^2-2\cdot8\cdot7.6\cdot\cos (A) \\ 25=64+57.76-121.6\text{ cos(A)} \\ 25=121.76-121.6(\cos A) \\ \text{subtract 121.76 in both sides} \\ 25-121.76=121.76-121.6(\cos A)-121.76 \\ -96.76=-121.6(\cos A) \\ \text{divide both sides by -121.6} \\ (-96.76)/(-121.6)=(-121.6(\cos A))/(-121.6) \\ 0.795=\cos \text{ (A)} \\ Inverse\text{ cosine} \\ \cos ^(-1)(0.795)=\cos ^(-1)(\cos \text{ (A))} \\ 37.276=\text{ A} \\ \text{rounded} \\ A=37\~\text{ =A} \end{gathered}]()
Step 3
Finally,let's find angle B
we can use the formula as we did in step 2 to find angle A, but also we can use this fact:
the sum of the internal angles in a triangle equals 180 ,so
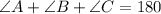
replace and solve for angle C