Question

riRick is creating I love version for Morty to make the potion Rick needs 51 mL of a mixture solution where 40% is carbonated water after checking around his job grapevines to Solutions he could use the first solution he found is 65% green tea and 15% carbonated water and 20% whole milk the second solution is 17% orange juice 38% lemonade and 45% carbonated water how much of the first solution in the second solution does Rick need to mix together to create the Love Potion round your final answer to one decimal place you may solve this problem using any method .

Answer 1

First Solution: 8.5mL

Second Solution: 42.5 mL

Step-by-step explanation:

Let us call x the number of mL of the first solution and y the number of mL of the second solution.

Now, from the fact that the final solution is 51 mL, we know that

`x+y=51`

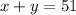
Furthermore, from the fact that the final solution 40% carbonated water, meaning there are in total

`51*(40)/(100)=20.4mL`

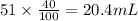
of carbonated water in the love potion.

Now, the first solution contributes 15/100 * x mL of carbonated water in the solution whereas the second solution contributes 45/100 * y mL. Since all 20.4 mL of carbonated water in the solution is coming from solution 1 and 2, then it must be that

`(15)/(100)x+(45)/(100)y=20.4`
`0.15x+0.45y=20.4`

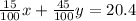
Thus we have two equations and two unknowns

`\begin{gathered} 0.15x+0.45y=20.4 \\ x+y=51 \end{gathered}`

We solve the above system by elimination.

First multiplying the second equation by 0.15 gives

`\begin{gathered} 0.15x+0.45y=20.4 \\ 0.15x+0.15y=51\cdot0.15 \end{gathered}`

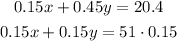
which simplifies to give

`\begin{gathered} 0.15x+0.45y=20.4 \\ 0.15x+0.15y=7.65 \end{gathered}`

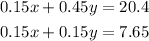
Subtracting the first equation from the second gives

`0.30y=12.75`

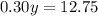
Finally, dividing both sides by 0.30 gives

`\boxed{y=42.5.}`

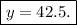
With the value of y in hand, we now put it into x+ y = 51 and solve to x to get

`x+42.5=51`

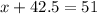
subtracting 42.5 from both sides gives

`\boxed{x=8.5.}`

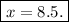
Hence, to conclude the needed amounts of the solution are:

First Solution: 8.5mL

Second Solution: 42.5 mL