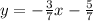First, find the slope of the line that passes through the given points using the slope formula:
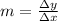
Next, substitute the value of the slope and the coordinates of one of the given points into the slope-intercept form of the equation of a line to find the y-intercept b:

Compute the value of the slope:
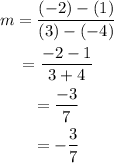
Replace m=-3/7, x=-4 and y=1 into the slope-intercept form of the equation of a line:
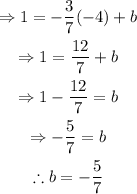
Replace m=-3/7 and b=-5/7 to get the equation of the line through the points (-4,1) and (3,-2):
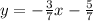
Therefore, the answer is: