Question

Use the values provided to calculate each of missing values (need to answer questions a-c pics attached)

Answer 1

b) The general point-slope equation of a line is:

`y=m\cdot(x-x_1)+y_1._{}`

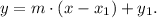
Where:

• (x1, y1) is a point of the line,

,

• m is the slope, given by:

`m=(y_2-y_1)/(x_2-x_1),`

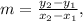
where (x1, y1) and (x2, y2) are two points of the line.

From the table, we have the points:

• (x1, y1) = (5.3, 17.46),

,

• (x2, y2) = (5.9, 17.70).

Replacing these values in the equation of the slope, we get:

`m=(17.70-17.46)/(5.9-5.3)=(0.24)/(0.6)=0.4.`

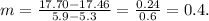
Replacing m = 0.4 and (x1, y1) = (5.3, 17.46) in the general equation of the line, we get:

`y=0.4\cdot(x-5.3)+17.46=0.4x-0.4\cdot5.3+17.46=0.4x+15.34.`

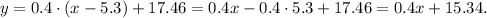
The equation of the line is:

`y=0.4x+15.34.`

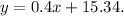
a) Using the equation of the line, we compute the blank values of y:

`\begin{gathered} x=5.6\rightarrow y=0.4\cdot5.6+15.34=17.58, \\ x=6.3\rightarrow y=0.4\cdot6.3+15.34=17.86, \\ x=8.3\rightarrow y=0.4\cdot8.3+15.34=18.66. \end{gathered}`

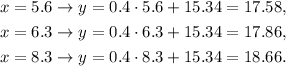
Replacing the value y = 18.00 in the equation of the line and solving for x, we get:

`\begin{gathered} 18.00=0.4x+15.34, \\ 0.4x=18.00-15.34, \\ 0.4x=2.66, \\ x=(2.66)/(0.4)=6.65. \end{gathered}`

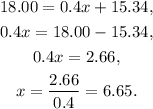
Answer

a) Table

• x = 5.6, y = ,17.58

,

• x = 6.3, y = ,17.86

,

• x = ,6.65,, y = 18.00

,

• x = 8.3, y = ,18.66

b) Equation of the line

y = 0.4x + 15.34

c) These values are the same as the ones in part (a)