Question

Two mirrors (M1, M2) make an angle of 120 ° between them. An incident ray makes with the mirror M1 an angle of 65 ° with respect to the normal of this one.Find the direction of the ray after its reflection on mirror M2.

Answer 1

First, let's make a diagram to visualize the problem.

According to the law of reflection, we know that

`\alpha=65`

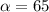
Also, these two angles are complementary so,

`\alpha+\lambda=90`

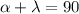
Let's find lambda.

`\begin{gathered} 65+\lambda=90 \\ \lambda=90-65 \\ \lambda=25 \end{gathered}`

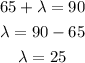
Now, we can find angle gamma using the interior angles of a theorem (triangle).

`\begin{gathered} \lambda+120+\gamma=180 \\ 25+120+\gamma=180 \\ \gamma=180-145 \\ \gamma=35 \end{gathered}`

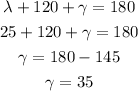
Then, we observe that angle gamma and angle beta are complementary, so let's find beta.

`\begin{gathered} \gamma+\beta=90 \\ 35+\beta=90 \\ \beta=90-35 \\ \beta=55 \end{gathered}`

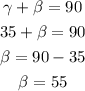
At last, by the law of reflection, we state that

`\theta=\beta=55`

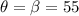
Therefore, the direction of the ray after its reflection on mirror M2 is 55.