From the question,
we have the table below
We are to find
1. mean
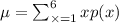
By inserting values we get
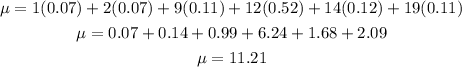
Therefore, mean = 11.21
2. Variance
The variance is given as
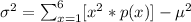
Inserting values we get

Therefore,
The variance is 21.706
3. Standard deviation
this is given as
![\sigma=\sqrt[]{\sigma^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1nil4daxtwmiiojjzy9q3k9t0m5jcp66vg.png)
Therefore,
![\begin{gathered} \sigma=\sqrt[]{21.7059} \\ \sigma=4.659 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sfw2nl7k9p41wjgf0j3lezd0kv6zljjtb0.png)
Therefore,
Standard Deviation = 4.659
Expected Value
The expected value is given as

By inserting values we have
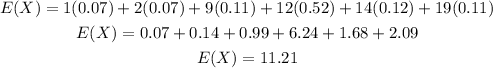
Therefore, the expected value is 11.21