Given:
The resistances in the series are,
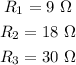
The potential of the battery is,
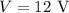
To find:
The current flow through the resistors
Step-by-step explanation:
The equivalent resistance is,
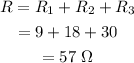
The current in all the resistors will be the same as the resistances are in a series combination.
The current is,
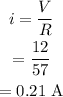
Hence, the current is 0.21 A.