Question

If B is the midpoint of AC, with point A at  (5, 2) and point C at (9, 0), what is the equation of the line perpendicular to AC that passes through B? A. y = - ½ x – 13 B. y = 2x – 13 C. y = - ½ x + 5 D. y = 2x + 5

Answer 1

The coordinates of point A, (x1, y1)=(5, 2).

The coordinates of point C, (x2, y2)=(9, 0).

Let (xm,ym) be the coordinates of the midpoint B.

Using midpoint formula, coordinates of the midpoint B can be found as,

`\begin{gathered} (x_m,y_m)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ =((5+9)/(2),\text{ }(2+0)/(2)) \\ =((14)/(2),\text{ 1)} \\ =(7,1) \end{gathered}`

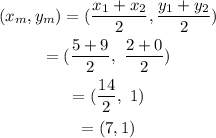
The slope of the line AC is,

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ =(0-2)/(9-5) \\ =(-2)/(4) \\ =(-1)/(2) \end{gathered}`

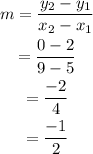
The slope of the line perpendicular to AC is,

`\begin{gathered} M=(-1)/(m) \\ =(-1)/((-1)/(2)) \\ =2 \end{gathered}`

Now using slope-point formula, the equation of a line perpendicular to AC and passing through point B can be found as,

`\begin{gathered} M=(y-y_m)/(x-x_m)\text{ (Slope-point formula)} \\ 2=(y-1)/(x-7) \\ 2x-7*2=y-1 \\ 2x-14=y-1 \\ 2x-13=y \end{gathered}`

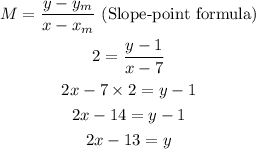
Therefore, the equation of a line perpendicular to AC and passing through point B is y=2x-13.