Given:
The slope (m) of the line given is,
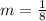
The point given is,
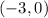
Required:
To draw the graph of the line that contains the given point and has the slope.
Step-by-step explanation:
We have the given point,
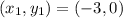
The slope of the line is,
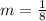
We know the slope-point form of the line given by,
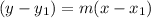
Therefore, using the given point and the slope in the above form, we get the equation of line as:
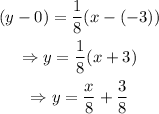
The graph of the line containing the given point and the slope is shown below:
Final Answer:
The equation of the line is,
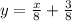
The graph of the line is shown in the attachment.