Answer:
5.1 days
Explanation:
The half-life of a substance is the time it takes the substance to decay to half of its initial mass.
The function that models the decay of the substance is:
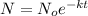
• The initial mass, No = 34 grams
,
• Half of the initial mass, N = 34/2 = 17 grams
,
• k=0.137
Substitute these values into the formula:
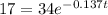
The equation is then solved for t:
![\begin{gathered} \text{ Divide both sides by 34} \\ (17)/(34)=(34e^(-0.137t))/(34) \\ e^(-0.137t)=0.5 \\ \text{ Take the }\ln\text{ of both sides} \\ \ln(e^(-0.137t))=\ln(0.5) \\ -0.137t=\ln(0.5) \\ \text{ Divide both sides by -0.137} \\ (-0.137t)/(-0.137)=\frac{\operatorname{\ln}(0.5)}{-0.137} \\ t=5.06 \\ t\approx5.1\text{ days} \end{gathered}]()
The substance's half-life is 5.1 days (rounded to the nearest tenth).