Question

Determining and behavior and intercepts to graph a polynomial function

Answer 1

Given a function:

`f(x)=(x-1)(x+2)(x+1)^2`

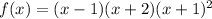
a)

The function approaches positive infinity when x approaches positive infinity and negative infinity as well.

Thus, the graph rises to the left and rises to the right is the correct option.

b)

We know that If the graph crosses the x-axis at a zero, it is a zero with odd multiplicity and If the graph touches the x-axis and bounces off of the axis, it is a zero with even multiplicity.

Here, the zero with odd multiplicity are x = 1 and x = -2. The zero with even multiplicity is x = -1.

Thus, the graph crosses x-axis at x = 1 and x = -2 and the graph touches, but does not cross the x-axis at x = -1.

c)

To find the y-intercept, replace x with 0.

`f(0)=(0-1)(0+2)(0+1)^2=-2`

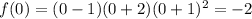
Thus, the y-intercept is at y = -2.

d)

Here. plot the points which intersects x-axis that are (1,0), (-2,0) and (-1,0). The point at which the graph intersects the y-axis is (0,-2).

The behavior of points that intersects x-axis is as follows:

At (1,0) and (-2,0) the graph passes through the x-axis.

At (-2,0) the graph touches the x-axis but not cross it.

The graph is given below: