Given:
Initial population = 12,000
Rate of increasing = 9% = 0.09
Required: Population after 7 years
Step-by-step explanation:
The population growth after t years is defined as
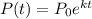
Substitute the given values into the formula.
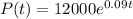
To find the population after 7 years, substitute 7 for t in P(t).
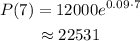
Final Answer: 22531 marsupials are there after 7 years