Given:
Height of the cylindrical pillar = 9 cm
Volume = 324π cm³
Recall,
Area of the circle (Base of the cylindrical pillar):
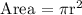
Volume of a cylinder:
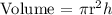
In other words, the formula for the pillar's volume will be:
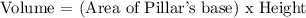
Where,
r = radius
h = height of the pillar
Thus, we get:
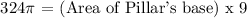
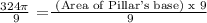
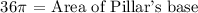
ANSWER: 36π cm²