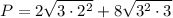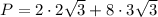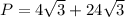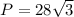Question

9. Find the perimeter of the rectangle. Write answer in simplest radical form. Show allwork.

Answer 1

`P=28√(3)`

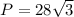
Step-by-step explanation

The perimeter is the addition of all the side's lengths.

As this is a rectangle, one pair of sides measures 4√27, and the other pair measures √12. Then, the perimeter P can be calculated as follows:

`P=√(12)+√(12)+4√(27)+4√(27)`

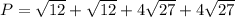
Simplifying:

`P=2√(12)+8√(27)`

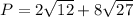
Now, we can further simplify by finding the factors of the numbers inside the square root:

`12=6\cdot2=3\cdot2\cdot2=3\cdot2^2`
`27=9\cdot3=3\cdot3\cdot3=3^2\cdot3`

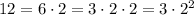
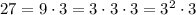
Then, substituting the factors inside the square root in the perimeter equation and simplifying:

`P=2√(3\cdot2^2)+8√(3^2\cdot3)`
`P=2\cdot2√(3)+8\cdot3√(3)`
`P=4√(3)+24√(3)`
`P=28√(3)`