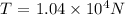Question

An undersea vessel is spherical with an external diameter of 5.20 meters. The mass of the vessel is 74,400 kg. It is anchored to the sea floor by a cable. density of sea water = 1.025x103 kg/m3 a) Draw a free-body diagram showing all forces. b) Calculate the buoyant force on the vessel. c) Calculate the tension in the cable.

Answer 1

Answer:
`\begin{gathered} \text{Buoyant Force on the vessel= 7.40}*10^5N \\ \text{Tension in the cable = 1.04}*10^4N \end{gathered}`

Explanations:

The mass of the vessel, m = 74400 kg

The external diameter, d = 5.20 m

Radius, r = 5.2 / 2 = 2.6 m

The volume of the vessel is given by the volume of a sphere

`\begin{gathered} V\text{ = }(4)/(3)\pi r^3 \\ V\text{ = }(4)/(3)*3.142*2.6^3 \\ V\text{ = }73.63m^3 \end{gathered}`

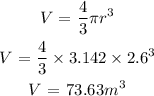
a) The buoyant force (B) is given by the formula:

`\begin{gathered} B\text{ = }\rho_wgV \\ B\text{ = 1025}*9.8*73.63 \\ B\text{ = }739613.35 \\ B\text{ = 740000 (to the nearest ten thousand)} \\ B\text{ = 7.40}*10^5N \end{gathered}`

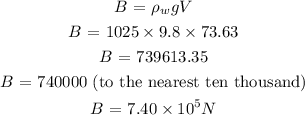
b) The tension in the cable is given by the equation

`T\text{= B - mg}`

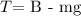
Where T represents the tension

T = 739613.35 - 74400(9.8)

T = 10493.35

`T\text{ = 1.04}*10^4N`