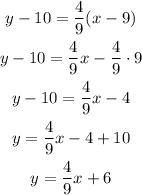Question

point A line passes through the points (-18, -2) and (9, 10). Find this line's equation in point-slope form A) Using the point (-18, -2), this line's point-siope form equation is a: B) Using the point (9, 10). This line's point-stope form equation is:

Answer 1

The line passes through points (-18,-2) and (9,10)

You have to find the equation of this line in point-slope form, which is:

`y-y_1=m(x-x_1)`

Where

m is the slope of the line

(x₁,y₁) are the coordinates of one point of the line.

Before writing the equation of the line, you have to calculate the slope of said line.

To calculate the slope you can use the following formula:

`m=(y_1-y_2)/(x_1-x_2)`

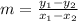
Where

(x₁,y₁) are the coordinates of one point of the line

(x₂,y₂) are the coordinates of a second point of the line

Using

(x₁,y₁) → (9,10)

(x₂,y₂) → (-18,-2)

You can calculate the slope as follows:

`\begin{gathered} m=(10-(-2))/(9-(-18)) \\ m=(10+2)/(9+18) \\ m=(12)/(27) \\ m=(4)/(9) \end{gathered}`

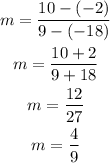
The slope of the line is m=4/9

Now you can write the equation in the point-slope form:

a)

(x₁,y₁) → (-18,-2)

m=4/9

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-2)=(4)/(9)(x-(-18)) \\ y+2=(4)/(9)(x+18) \end{gathered}`

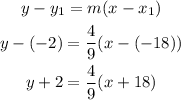
The equation in the point-slope form using the point (-18,-2) is:

`y+2=(4)/(9)(x+18)`

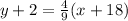
Slope-intercept form:

`\begin{gathered} y+2=(4)/(9)(x+18) \\ y+2=(4)/(9)x+(4)/(9)\cdot18 \\ y+2=(4)/(9)x+8 \\ y=(4)/(9)x+8-2 \\ y=(4)/(9)x+6 \end{gathered}`

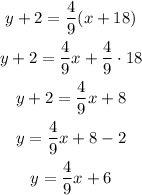
b)

(x₁,y₁) → (9,10)

m=4/9

`\begin{gathered} y-y_1=m(x-x_1) \\ y-10=(4)/(9)(x-9) \end{gathered}`

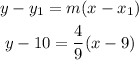
The equation in the point-slope form using the point (9,10) is:

`y-10=(4)/(9)(x-9)`

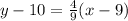
Slope-intercept form:

`\begin{gathered} y-10=(4)/(9)(x-9) \\ y-10=(4)/(9)x-(4)/(9)\cdot9 \\ y-10=(4)/(9)x-4 \\ y=(4)/(9)x-4+10 \\ y=(4)/(9)x+6 \end{gathered}`